Methodology for Research¶

In this chapter the methodology used for investigating the influences of BEV loading on the local grid is beeing discussed. This methodology is separated into 7 parts:

choosing and implementing a reference grid
choosing and implementing of a standard load profile (SLP) for the households
implementing a model for charging of BEV battery
choosing and implementig of a distribution of arrival times for BEVs
choosing and implementing of a distribution for the travelled distances
choosing and implementing of a distribution for the nominal powers of the charging stations
additionally a controller is beeing designed

The Reference Grid¶

The reference grid used for the simulation is a kerber network as it is provided by pandapower. The following Figure 2 shows a schematic plot of the grid:

https://pandapower.readthedocs.io/en/develop/_images/kerber_vorstadtnetz_a.PNG

Fig. 2 The kerber network used for simulation¶

This network represents the average network in German suburbs as derived in [Ker11]. All the loads attached are households.

The Standard Load Profile¶

As a SLP serves a profile “H0A” of N_ERGIE netz of 2020, which represents the load of a household. The day with the highest power demand is the 13.12.2020. This day was choosen for the simulation. The following Figure 3 shows the SLP:

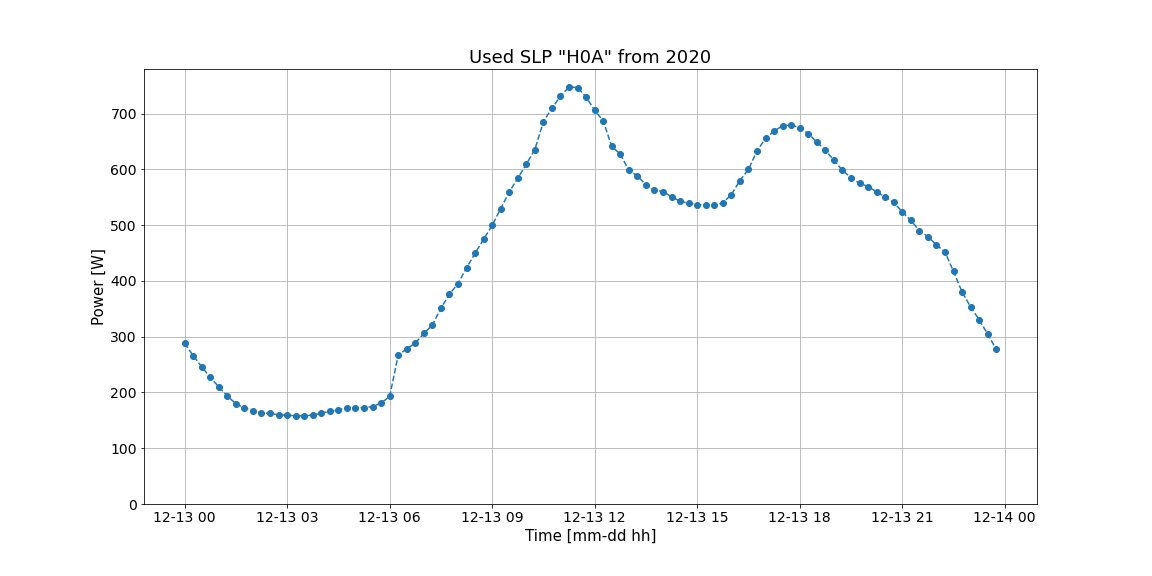
Fig. 3 Load profile of the used SLP¶

The values are considered to be real power.

The Model for charging BEV battery¶

The charging of the BEV battery is modelled according to [Sch08] wich is given by the following equations:

(1)¶\[P(SOC) = P_{max} \cdot e^{\left ( \tfrac{s - SOC}{k_L} \right )}\]

(2)¶\[k_L = \frac{100-s}{ln (\frac{P_{max}}{P_{LS}})}\]

(3)¶\[P_{LS} = \frac{U_{LS}}{U_N} \cdot I_{LS} \cdot E_{nom}\]

With the symbols beeing:

Symbol	Meaning	Unit
\(P\)	Power	\(W\)
\(P_{max}\)	Maximum Power	\(W\)
\(s\)	Switching Point	\(\%\)
\(SOC\)	State of Charge	\(\%\)
\(U_{LS}\)	Load-stop Voltage	\(V\)
\(U_N\)	Nominal Voltage	\(V\)
\(I_{LS}\)	Load-stop Current	\(\frac{1}{h}\)
\(E_N\)	Nominal Energy	Wh

The Nominal Voltage of Lithium-Ion-Batteries is expected to be \(U_N= 3.9V\), the Load-stop Voltage is taken as \(U_{LS}=4.2V\), the Load-stop Current is taken as \(I_{LS} = 0.03 \frac{1}{h}\) (c-rate) and the Switching Point is taken as \(s = 80\%\).

The following Figure 4 shows the loading curve as described by Equation (1):

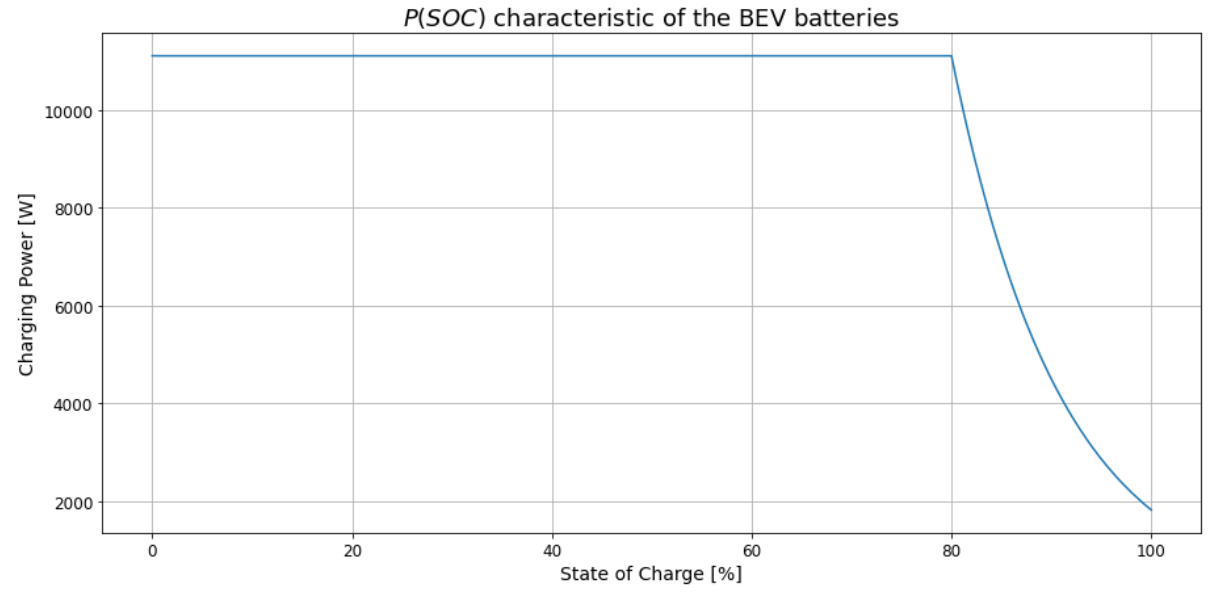
Fig. 4 Characteristic of the BEV batteries loading¶

It is to see, that the initial charging power is determined by the initial state of charge \(SOC_0\), which is calculated in dependence of the travelled distance \(d\) and the consumption \(c\) according the following Equation (4):

(4)¶\[SOC_0 = \frac{E_N - d \cdot c}{E_N} \cdot 100\%\]

The state of charge in the next discrete timestep \(SOC_{n+1}\) is calculated in dependence of the timestep \(\Delta t\) according the next Equation (5):

(5)¶\[SOC_{n+1} = SOC_n + P(SOC_n) \cdot \Delta t\]

The Distribution of Arrival Times¶

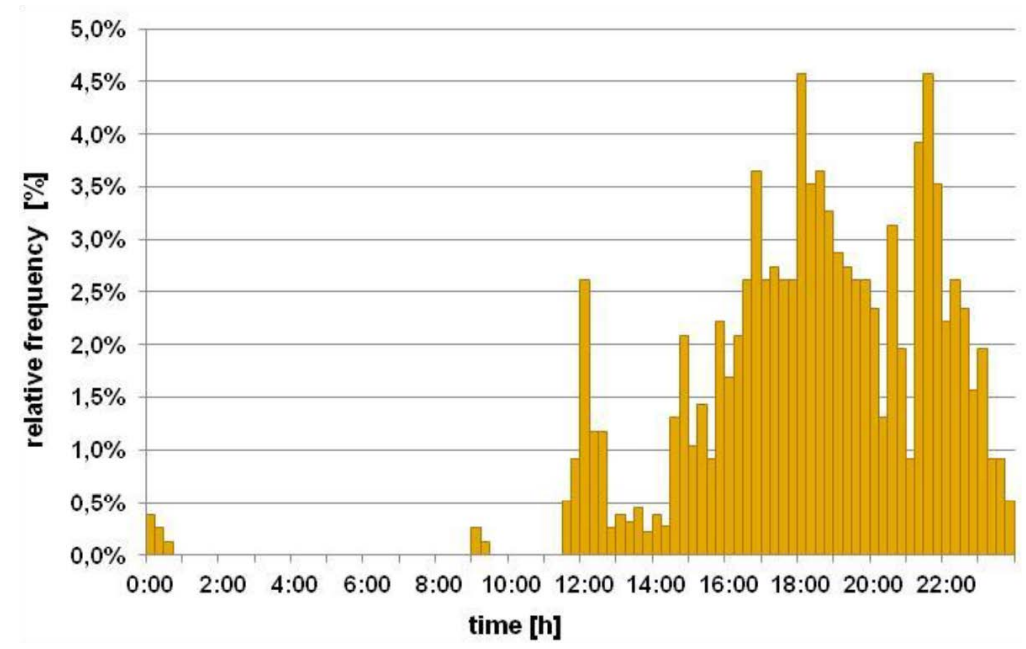
The distribution of arrival times is beeing adopted from [Dou15]. The following Figure 5 shows the distribution:

Fig. 5 Distribution of the arrival time [Dou15]¶

It ist to see, that most people arrive at 18:00 and there is also another peak at 22:00.

The Distribution of travelled Distances¶

The distribution of the travelled distances is taken from [sta]. The vaues provided for 2020 are downscaled to one day (assuming 365 days driving per year). These downscaled values are given in the following Table 3:

Table 3 Distribution of travelled distances¶
Distance travelled [km]	Probability [-]
7	0.13
21	0.29
35	0.30
50	0.15
60	0.13

These values determine the \(d\) in Equation (4). Furthermore the mean consumption of BEVs is taken as \(c=17.7 \frac{kWh}{100km}\) and the battery capacity as \(E_{nom}=52kWh\) (Values of the most sold BEV [ADA] according to [Ren]).

The Distribution of the Nominal Power of the Charging Stations¶

The distribution is taken from [goi], only taken into account the first three categories. This results in the values given in the following Table 4:

Table 4 Distribution of the charging power¶
Charging power [kW]	Probability
3.7	0.35
11.1	0.55
22.2	0.10

These values determine the \(P_{max}\) in Equation (1).

The controller¶

As a controller serves as a \(P(U)\) controlling according the characteristic in the following Figure 6:

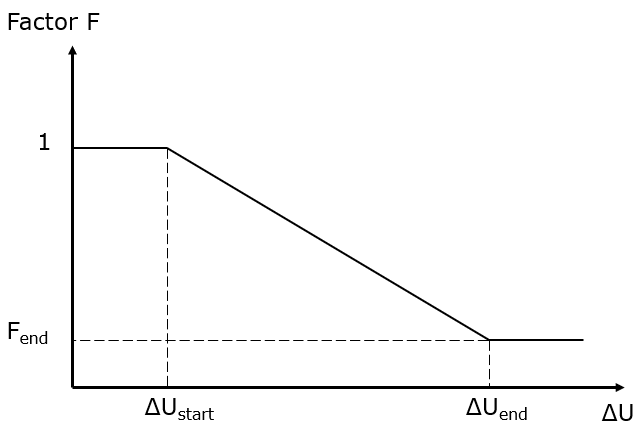
Fig. 6 Characteristic of the controller¶

The characteristic represents the P-element of the controller. The voltage drop \(\Delta U\) is defied according Equation (6):

(6)¶\[\Delta U = \frac{400V - U_{node}}{400V} \cdot 100\%\]

Furthermore an I-element is used defined in Equation (7):

(7)¶\[F_I = K_I \cdot \sum_{t-n}^{t} \Delta U(t)\]

And additionally a D-Element contributes to the controller according to Equation (8):

(8)¶\[F_D = K_D \cdot (\Delta U (t) - \Delta U (t-1))\]

This results in a controlled power \(P_{control}\) according to Equation (9):

(9)¶\[P_{control} = P \cdot (F - F_D - F_I)\]

The complete control loop is shown in the following Figure 7.

Fig. 7 Controller loop¶

The following Table 5 list all the adjustable parameters of the controller:

Table 5 Parameters of the controller¶
Parameter	Meaning	Default value
\(F_{end}\)	Factor at \(\Delta U_{end}\)	0.4
\(\Delta U_{start}\)	Voltage to start to lower charging power	0.01
\(\Delta U_{end}\)	Voltage to stop to lower charging power	0.06
\(K_D\)	Differential proportionality factor	0
\(K_I\)	Integration proportionality factor	0.5
\(n\)	Number of last values to calculate integral	15

Effects of different penetrations of BEV in suburban areas on the grid stability